
Reg. 8. Inventis longitudinibus AH , HX; si jam desideretur positio rectæ AH , secundum quam Projectile data illa cum velocitate emissum incidit in punctum quodvis K: ad puncta A & K erigantur rectæ AC, KF horizonti perpendiculares, quarum AC deorsum tendat, & æquetur ipsi AI seu HX. Asymptotis AK, KF describatur Hyperbola, cujus Conjugata transeat per punctum C, centroq; A & intervallo AH describatur Circulus secans Hyperbo lam illam in puncto H ; & projectile secundum rectam AH emissum incidet in punctum K. Q. E. I. Nam punctum H, ob datam longitudinem AH, locatur alicubi in circulo descripto. Agatur CH occurrens ipsis AK & KF, illi in C, huic in F, & ob parallelas CH, MX & æquales AC, AI, erit AE æqualis AM, & propterea etiam æqualis KN. Sed CE est ad AE ut FH ad KN, & propterea CE & FH æquantur. Incidit ergo punctum H in Hyperbolam Asymptotis AK, KF descriptam, cujus conjugata transit per punctum C, atq; adeo reperitur in communi intersectione Hyperbolæ hujus & circuli descripti. Q. E. D. Notandum est autem quod hæc operatio perinde se habet, sive recta AKN horizonti parallela sit, sive ad horizontem in angulo quovis inclinata: quodq; ex duabus intersectionibus H, H duo prodeunt anguli NAH, NAH, quorum minor eligendus est; & quod in Praxi mechanica sufficit circulum semel describere, deinde regulam interminatam CH ita applicare ad punctum C, ut ejus pars FH, circulo & rectæ FK interjecta, æqualis sit ejus parti CE inter punctum C & rectam HK sitæ.
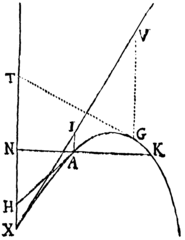
Quæ de Hyperbolis dicta sunt facile applicantur ad Parabolas. Nam si XAGK Parabolam designet quam recta XV tangat in vertice X, sintq; ordinatim applicatæ I A, VG ut quælibet abscissarum XI, XV dignitates ; agantur XT, TG, HA, quarum XT parallela sit VG, & TG, HA parabolam tangant in G & A: & corpus de loco quovis A, secundum rectam AH productam, justa cum velocitate projectum, describet hanc Parabolam, si modo densitas Medij, in locis singulis G, sit reciproce ut tangens GT. Velocitas autem in G ea erit quacum Projectile pergeret, in spatio non resistente, in Parabola Conica, verticem G, diametrum VG deorsum productam, & latus rectum habente. Et resistentia in G erit ad vim Gravitatis ut TG ad . Vnde si NAK lineam horizontalem designet, & manente tum densitate Medij in A, tum velocitate quacum corpus projicitur, mutetur utcunq; angulus NAH; manebunt longitudines AH, AI, HX, & inde datur




